Posts

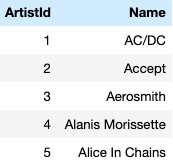
The relational model and skew lattices, Part II

In our previous post we established a connection between skew lattices and the relational model in data science. It is thus time to answer the following question: What exactly are skew lattices? A skew lattice is a set S equipped with a pair of binary operations ∧ ( meet ) and ∨ ( join ) such that given any x, y, z in S the following identities hold: x ∧ x = x     idempotency of meet x  ∨  x  =  x     idempotency of join ( x  ∧  y ) ∧ z = x  ∧ ( y  ∧  z )    associativity of meet ( x  ∨  y ) ∨  z  =  x  ∨ ( y  ∨  z )    associativity of join x  ∧ ( x  ∨  y ) = x =  x  ∨ ( x  ∧  y )    absorption ( x  ∧  y ) ∨  y  = y = ( x  ∨  y ) ∧  y     absorption Noncommutative (in the inclusive sense as in "not necessarily commutative") lattices  were first introduced by a German physicist Pascual Jordan in 1949, however the modern theory of skew lattices is due to the extensive study developed mainly by Jonathan Leech and initiated in the paper: J. Leech, Skew lattices in rings
Post a Comment
Read more

The relational model and skew lattices, Part I

Image
So, how about noncommutative lattices in data science? The aim of this post is to demonstrate a connection between data science and noncommutative lattices, more precisely skew lattices. This is work in progress. The relational model is one of the most basic models used in data science. Data is organized into tables called relations , each being composed of rows and columns. Columns correspond to attributes, while rows correspond to data entries. Rows are often referred to as  records . In data science, a database organized as a relational model can be manipulated for instance with the SQL (pronounce: "sequel") language.  Let's look at an example. The open source  Chinook database  represents a digital media store with the media related data collected from the iTunes Library. It is composed of several tables like artists, albums, tracks, genres etc. In order to get some insight into the database, let's look at the first five records of the following tables: artists
Post a Comment
Read more

Pointex

( This post is a continuation of the post  Oscar on the island of two truths . ) It was a funny little dwarf called Pointex that explained to Oscar all the basics about the reasoning on the island. "Are the queen and the king very smart?" asked Oscar. "Of course they're smart! Some even believe that the queen and the king are right about everything!" said Pointex proudly. Exercise 3 . Show that if the queen and the king are right about everything then they must agree on everything. Exercise 4. Note that if the queen and the king both believe p then they don't agree on p! "Is there a way to tell who agrees with who?" asked Oscar. "It seems to me that the queen and the king don't agree on anything!" He was astonished by the strange relations that seemed to rule the island. "Oh, no, of course they do!" said Pointex who was now amusing himself by jumping around Oscar balancing on his left foot. Exercise 5. Show that if the que
Post a Comment
Read more

Oscar on the island of two truths

Imagine that one day you woke up in a world having another logic underling all our thinking and all our reasoning. That is exactly what happened to Oscar on a murky winter day when he was playing with his magic set, picturing himself as Harry Potter fighting with Voldemort. Suddenly he found himself on an island inhabited by people who had a way of thinking completely different from anything he had ever encountered before. Instead of the two truth values 0 and 1 as in the world he used to live in, there were three: 0, Q and K . For the people of the island the proposition " Oscar is a ten-year-old. " wasn't either TRUE or FALSE, but rather Q -TRUE, K -TRUE or FALSE. How exactly are we to understand that, and how did it effect the interactions among the inhabitants of the island? And how was Oscar to explain to the people of the island that he really was  ten years old? The island was ruled by a queen and a king. It is important to stress that the queen was neither infer
Post a Comment
Read more

Puzzles and nonclassical logic

All happy families are alike; each unhappy family is unhappy in its own way. Lev Nikolayevich Tolstoy, Anna Karenina  Applying the famous beginning of one of the finest novels of all times to logics, there is no doubt that classical logic plays the role of happy families, while nonclassical logics get to play the unfortunate, yet intriguing parts of unhappy families. Put otherwise, there are plenty generalizations of classical logic all gathered under the same roof named "nonclassical logic", which often differ one from another at least as much as they differ from the "happy" classical logic. Probably the most fundamental property of classical logic is that there are exactly two truth values: 1 and 0. Moreover, any given statement is either TRUE or FALSE (though maybe we do not always know which). This concept is very natural and something that humans tend to a priori assume. If anything, this must hold. Historically speaking, mathematicians also used to assume thi
Post a Comment
Read more

My very first post

The emphasis of this blog is meant to be on the "Beyond" arising from maths. Being a professional mathematician, as I started studying data science about a year ago, I was surprised to discover connections with maths that I had not anticipated. Surely, I knew that data science was in a way all about maths. I've heard people say that it was just a fancy word (or two) for applied statistics. What surprised me was thus not that maths was involved, but rather that I've encountered areas of maths which had nothing to do with statistics and thus I didn't expect to run into them in connection to data science. Like noncommutative lattices, for example. But more about this in the posts to follow. Logical puzzles In this very first post I would like to share another "beyond", also connected to noncommutative lattices, an application of maths that's obsessed me for quite some time. Let's call them 'noncommutative logical puzzles', if you want. Hold
Post a Comment
Read more