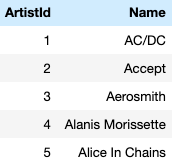
The relational model and skew lattices, Part II
In our previous post we established a connection between skew lattices and the relational model in data science. It is thus time to answer the following question: What exactly are skew lattices? A skew lattice is a set S equipped with a pair of binary operations ∧ ( meet ) and ∨ ( join ) such that given any x, y, z in S the following identities hold: x ∧ x = x idempotency of meet x ∨ x = x idempotency of join ( x ∧ y ) ∧ z = x ∧ ( y ∧ z ) associativity of meet ( x ∨ y ) ∨ z = x ∨ ( y ∨ z ) associativity of join x ∧ ( x ∨ y ) = x = x ∨ ( x ∧ y ) absorption ( x ∧ y ) ∨ y = y = ( x ∨ y ) ∧ y absorption Noncommutative (in the inclusive sense as in "not necessarily commutative") lattices wer...